HM Medical Clinic

Odds are, it's wrong - science news

Home / March 27th, 2010; Vol.177 #7 / Feature Odds Are, It's Wrong
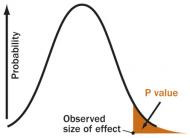
Science fails to face the shortcomings of statistics March 27th, 2010; Vol.177 #7 (p. 26) P VALUE
A P value is the probability of an observed (or more extreme)
result arising only from chance.
S. Goodman, adapted by A. Nandy For better or for worse, science has long been married tomathematics. Generally it has been for the better. Especially sincethe days of Galileo and Newton, math has nurtured science. Rigorousmathematical methods have secured science's fidelity to fact andconferred a timeless reliability to its findings.
During the past century, though, a mutant form of math hasdeflected science's heart from the modes of calculation that had longserved so faithfully. Science was seduced by statistics, the mathrooted in the same principles that guarantee profits for Las Vegascasinos. Supposedly, the proper use of statistics makes relying onscientific results a safe bet. But in practice, widespread misuse ofstatistical methods makes science more like a crapshoot.
It's science's dirtiest secret: The "scientific method" of testinghypotheses by statistical analysis stands on a flimsy foundation.
Statistical tests are supposed to guide scientists in judging whetheran experimental result reflects some real effect or is merely arandom fluke, but the standard methods mix mutually inconsistentphilosophies and offer no meaningful basis for making suchdecisions. Even when performed correctly, statistical tests are widelymisunderstood and frequently misinterpreted. As a result, countlessconclusions in the scientific literature are erroneous, and tests ofmedical dangers or treatments are often contradictory and confusing.
Replicating a result helps establish its validity more securely, but thecommon tactic of combining numerous studies into one analysis,while sound in principle, is seldom conducted properly in practice.
Experts in the math of probability and statistics are well aware ofthese problems and have for decades expressed concern about themin major journals. Over the years, hundreds of published papers havewarned that science's love affair with statistics has spawnedcountless illegitimate findings. In fact, if you believe what you readin the scientific literature, you shouldn't believe what you read in thescientific literature.
"There is increasing concern," declared epidemiologist John Ioannidisin a highly cited 2005 paper in PLoS Medicine, "that in modernresearch, false findings may be the majority or even the vastmajority of published research claims." Ioannidis claimed to prove that more than half of published findingsare false, but his analysis came under fire for statisticalshortcomings of its own. "It may be true, but he didn't prove it,"says biostatistician Steven Goodman of the Johns Hopkins UniversitySchool of Public Health. On the other hand, says Goodman, the basicmessage stands. "There are more false claims made in the medicalliterature than anybody appreciates," he says. "There's no questionabout that." Nobody contends that all of science is wrong, or that it hasn'tcompiled an impressive array of truths about the natural world. Still,any single scientific study alone is quite likely to be incorrect, thankslargely to the fact that the standard statistical system for drawingconclusions is, in essence, illogical. "A lot of scientists don'tunderstand statistics," says Goodman. "And they don't understandstatistics because the statistics don't make sense." Nowhere are the problems with statistics more blatant than instudies of genetic influences on disease. In 2007, for instance,researchers combing the medical literature found numerous studieslinking a total of 85 genetic variants in 70 different genes to acutecoronary syndrome, a cluster of heart problems. When theresearchers compared genetic tests of 811 patients that had thesyndrome with a group of 650 (matched for sex and age) that didn't,only one of the suspect gene variants turned up substantially moreoften in those with the syndrome — a number to be expected bychance.
"Our null results provide no support for the hypothesis that any ofthe 85 genetic variants tested is a susceptibility factor" for thesyndrome, the researchers reported in the Journal of the AmericanMedical Association.
How could so many studies be wrong? Because their conclusionsrelied on "statistical significance," a concept at the heart of themathematical analysis of modern scientific experiments.
Statistical significance is a phrase that every science graduate student learns, but few comprehend. While its origins stretch back atleast to the 19th century, the modern notion was pioneered by themathematician Ronald A. Fisher in the 1920s. His original interestwas agriculture. He sought a test of whether variation in crop yieldswas due to some specific intervention (say, fertilizer) or merelyreflected random factors beyond experimental control.
Fisher first assumed that fertilizer caused no difference — the "noeffect" or "null" hypothesis. He then calculated a number called the Pvalue, the probability that an observed yield in a fertilized fieldwould occur if fertilizer had no real effect. If P is less than .05 —meaning the chance of a fluke is less than 5 percent — the resultshould be declared "statistically significant," Fisher arbitrarilydeclared, and the no effect hypothesis should be rejected,supposedly confirming that fertilizer works.
Fisher's P value eventually became the ultimate arbiter of credibilityfor science results of all sorts — whether testing the health effects ofpollutants, the curative powers of new drugs or the effect of geneson behavior. In various forms, testing for statistical significancepervades most of scientific and medical research to this day.
But in fact, there's no logical basis for using a P value from a singlestudy to draw any conclusion. If the chance of a fluke is less than 5percent, two possible conclusions remain: There is a real effect, orthe result is an improbable fluke. Fisher's method offers no way toknow which is which. On the other hand, if a study finds nostatistically significant effect, that doesn't prove anything, either.
Perhaps the effect doesn't exist, or maybe the statistical test wasn'tpowerful enough to detect a small but real effect.
"That test itself is neither necessary nor sufficient for proving ascientific result," asserts Stephen Ziliak, an economic historian atRoosevelt University in Chicago.
Soon after Fisher established his system of statistical significance, itwas attacked by other mathematicians, notably Egon Pearson andJerzy Neyman. Rather than testing a null hypothesis, they argued, itmade more sense to test competing hypotheses against one another.
That approach also produces a P value, which is used to gauge thelikelihood of a "false positive" — concluding an effect is real when itactually isn't. What eventually emerged was a hybrid mix of themutually inconsistent Fisher and Neyman-Pearson approaches, whichhas rendered interpretations of standard statistics muddled at bestand simply erroneous at worst. As a result, most scientists areconfused about the meaning of a P value or how to interpret it. "It'salmost never, ever, ever stated correctly, what it means," saysGoodman.
Correctly phrased, experimental data yielding a P value of .05 meansthat there is only a 5 percent chance of obtaining the observed (ormore extreme) result if no real effect exists (that is, if theno-difference hypothesis is correct). But many explanations mangle the subtleties in that definition. A recent popular book on issuesinvolving science, for example, states a commonly heldmisperception about the meaning of statistical significance at the .05level: "This means that it is 95 percent certain that the observeddifference between groups, or sets of samples, is real and could nothave arisen by chance." That interpretation commits an egregious logical error (technicalterm: "transposed conditional"): confusing the odds of getting aresult (if a hypothesis is true) with the odds favoring the hypothesisif you observe that result. A well-fed dog may seldom bark, butobserving the rare bark does not imply that the dog is hungry. A dogmay bark 5 percent of the time even if it is well-fed all of the time.
(See Box 2) Another common error equates statistical significance to"significance" in the ordinary use of the word. Because of the waystatistical formulas work, a study with a very large sample candetect "statistical significance" for a small effect that is meaninglessin practical terms. A new drug may be statistically better than an olddrug, but for every thousand people you treat you might get just oneor two additional cures — not clinically significant. Similarly, whenstudies claim that a chemical causes a "significantly increased risk ofcancer," they often mean that it is just statistically significant,possibly posing only a tiny absolute increase in risk.
Statisticians perpetually caution against mistaking statisticalsignificance for practical importance, but scientific papers committhat error often. Ziliak studied journals from various fields —psychology, medicine and economics among others — and reportedfrequent disregard for the distinction.
"I found that eight or nine of every 10 articles published in theleading journals make the fatal substitution" of equating statisticalsignificance to importance, he said in an interview. Ziliak's data aredocumented in the 2008 book The Cult of Statistical Significance,coauthored with Deirdre McCloskey of the University of Illinois atChicago.
Multiplicity of mistakes
Even when "significance" is properly defined and P values arecarefully calculated, statistical inference is plagued by many otherproblems. Chief among them is the "multiplicity" issue — the testingof many hypotheses simultaneously. When several drugs are testedat once, or a single drug is tested on several groups, chances ofgetting a statistically significant but false result rise rapidly.
Experiments on altered gene activity in diseases may test 20,000genes at once, for instance. Using a P value of .05, such studiescould find 1,000 genes that appear to differ even if none are actuallyinvolved in the disease. Setting a higher threshold of statisticalsignificance will eliminate some of those flukes, but only at the costof eliminating truly changed genes from the list. In metabolic diseases such as diabetes, for example, many genes truly differ inactivity, but the changes are so small that statistical tests willdismiss most as mere fluctuations. Of hundreds of genes thatmisbehave, standard stats might identify only one or two. Alteringthe threshold to nab 80 percent of the true culprits might produce alist of 13,000 genes — of which over 12,000 are actually innocent.
Recognizing these problems, some researchers now calculate a "falsediscovery rate" to warn of flukes disguised as real effects. Andgenetics researchers have begun using "genome-wide associationstudies" that attempt to ameliorate the multiplicity issue (SN:6/21/08, p. 20).
Many researchers now also commonly report results with confidenceintervals, similar to the margins of error reported in opinion polls.
Such intervals, usually given as a range that should include theactual value with 95 percent confidence, do convey a better sense ofhow precise a finding is. But the 95 percent confidence calculation isbased on the same math as the .05 P value and so still shares someof its problems.
Clinical trials and errors
Statistical problems also afflict the "gold standard" for medicalresearch, the randomized, controlled clinical trials that test drugs fortheir ability to cure or their power to harm. Such trials assignpatients at random to receive either the substance being tested or aplacebo, typically a sugar pill; random selection supposedlyguarantees that patients' personal characteristics won't bias thechoice of who gets the actual treatment. But in practice, selectionbiases may still occur, Vance Berger and Sherri Weinstein noted in2004 in ControlledClinical Trials. "Some of the benefits ascribed torandomization, for example that it eliminates all selection bias, canbetter be described as fantasy than reality," they wrote.
Randomization also should ensure that unknown differences amongindividuals are mixed in roughly the same proportions in the groupsbeing tested. But statistics do not guarantee an equal distributionany more than they prohibit 10 heads in a row when flipping apenny. With thousands of clinical trials in progress, some will not bewell randomized. And DNA differs at more than a million spots in thehuman genetic catalog, so even in a single trial differences may notbe evenly mixed. In a sufficiently large trial, unrandomized factorsmay balance out, if some have positive effects and some arenegative. (See Box 3) Still, trial results are reported as averagesthat may obscure individual differences, masking beneficial or harm-ful effects and possibly leading to approval of drugs that are deadlyfor some and denial of effective treatment to others.
"Determining the best treatment for a particular patient isfundamentally different from determining which treatment is best onaverage," physicians David Kent and Rodney Hayward wrote inAmerican Scientist in 2007. "Reporting a single number gives the misleading impression that the treatment-effect is a property of thedrug rather than of the interaction between the drug and thecomplex risk-benefit profile of a particular group of patients."Another concern is the common strategy of combining results frommany trials into a single "meta-analysis," a study of studies. In asingle trial with relatively few participants, statistical tests may notdetect small but real and possibly important effects. In principle,combining smaller studies to create a larger sample would allow thetests to detect such small effects. But statistical techniques for doingso are valid only if certain criteria are met. For one thing, all thestudies conducted on the drug must be included — published andunpublished. And all the studies should have been performed in asimilar way, using the same protocols, definitions, types of patientsand doses. When combining studies with differences, it is necessaryfirst to show that those differences would not affect the analysis,Goodman notes, but that seldom happens. "That's not a formal partof most meta-analyses," he says.
Meta-analyses have produced many controversial conclusions.
Common claims that antidepressants work no better than placebos,for example, are based on meta-analyses that do not conform to thecriteria that would confer validity. Similar problems afflicted a 2007meta-analysis, published in the New England Journal of Medicine,that attributed increased heart attack risk to the diabetes drugAvandia. Raw data from the combined trials showed that only 55people in 10,000 had heart attacks when using Avandia, comparedwith 59 people per 10,000 in comparison groups. But after a seriesof statistical manipulations, Avandia appeared to confer an increasedrisk.
In principle, a proper statistical analysis can suggest an actual riskeven though the raw numbers show a benefit. But in this case thecriteria justifying such statistical manipulations were not met. Insome of the trials, Avandia was given along with other drugs.
Sometimes the non-Avandia group got placebo pills, while in othertrials that group received another drug. And there were no commondefinitions.
"Across the trials, there was no standard method for identifying orvalidating outcomes; events . may have been missed ormisclassified," Bruce Psaty and Curt Furberg wrote in an editorialaccompanying the New England Journal report. "A few events eitherway might have changed the findings." More recently, epidemiologist Charles Hennekens and biostatisticianDavid DeMets have pointed out that combining small studies in ameta-analysis is not a good substitute for a single trial sufficientlylarge to test a given question. "Meta-analyses can reduce the role ofchance in the interpretation but may introduce bias andconfounding," Hennekens and DeMets write in the Dec. 2 Journal ofthe American Medical Association. "Such results should be consideredmore as hypothesis formulating than as hypothesis testing." These concerns do not make clinical trials worthless, nor do theyrender science impotent. Some studies show dramatic effects thatdon't require sophisticated statistics to interpret. If the P value is0.0001 — a hundredth of a percent chance of a fluke — that is strongevidence, Goodman points out. Besides, most well-accepted scienceis based not on any single study, but on studies that have beenconfirmed by repetition. Any one result may be likely to be wrong,but confidence rises quickly if that result is independently replicated.
"Replication is vital," says statistician Juliet Shaffer, a lectureremeritus at the University of California, Berkeley. And in medicine,she says, the need for replication is widely recognized. "But in thesocial sciences and behavioral sciences, replication is not common,"she noted in San Diego in February at the annual meeting of theAmerican Association for the Advancement of Science. "This is a sadsituation." Bayes watch
Such sad statistical situations suggest that the marriage of scienceand math may be desperately in need of counseling. Perhaps it couldbe provided by the Rev. Thomas Bayes.
Most critics of standard statistics advocate the Bayesian approach tostatistical reasoning, a methodology that derives from a theoremcredited to Bayes, an 18th century English clergyman. His approachuses similar math, but requires the added twist of a "priorprobability" — in essence, an informed guess about the expectedprobability of something in advance of the study. Often this priorprobability is more than a mere guess — it could be based, forinstance, on previous studies.
Bayesian math seems baffling at first, even to many scientists, but itbasically just reflects the need to include previous knowledge whendrawing conclusions from new observations. To infer the odds that abarking dog is hungry, for instance, it is not enough to know howoften the dog barks when well-fed. You also need to know how oftenit eats — in order to calculate the prior probability of being hungry.
Bayesian math combines a prior probability with observed data toproduce an estimate of the likelihood of the hunger hypothesis. "Ascientific hypothesis cannot be properly assessed solely by referenceto the observational data," but only by viewing the data in light ofprior belief in the hypothesis, wrote George Diamond and SanjayKaul of UCLA's School of Medicine in 2004 in the Journal of theAmerican College of Cardiology. "Bayes' theorem is . a logicallyconsistent, mathematically valid, and intuitive way to drawinferences about the hypothesis." (See Box 4) With the increasing availability of computer power to perform itscomplex calculations, the Bayesian approach has become morewidely applied in medicine and other fields in recent years. In manyreal-life contexts, Bayesian methods do produce the best answers to important questions. In medical diagnoses, for instance, thelikelihood that a test for a disease is correct depends on theprevalence of the disease in the population, a factor that Bayesianmath would take into account.
But Bayesian methods introduce a confusion into the actual meaningof the mathematical concept of "probability" in the real world.
Standard or "frequentist" statistics treat probabilities as objectiverealities; Bayesians treat probabilities as "degrees of belief" based inpart on a personal assessment or subjective decision about what toinclude in the calculation. That's a tough placebo to swallow forscientists wedded to the "objective" ideal of standard statistics.
"Subjective prior beliefs are anathema to the frequentist, who reliesinstead on a series of ad hoc algorithms that maintain the facade ofscientific objectivity," Diamond and Kaul wrote.
Conflict between frequentists and Bayesians has been ongoing fortwo centuries. So science's marriage to mathematics seems to entailsome irreconcilable differences. Whether the future holds a fruitfulreconciliation or an ugly separation may depend on forging a sharedunderstanding of probability.
"What does probability mean in real life?" the statistician DavidSalsburg asked in his 2001 book The Lady Tasting Tea. "This problemis still unsolved, and . if it remains unsolved, the whole of thestatistical approach to science may come crashing down from theweight of its own inconsistencies." BOX 1: Statistics Can Confuse Statistical significance is not always statistically significant.
It is common practice to test the effectiveness (or dangers) of a drugby comparing it to a placebo or sham treatment that should have noeffect at all. Using statistical methods to compare the results,researchers try to judge whether the real treatment's effect wasgreater than the fake treatments by an amount unlikely to occur bychance.
By convention, a result expected to occur less than 5 percent of thetime is considered "statistically significant." So if Drug Xoutperformed a placebo by an amount that would be expected bychance only 4 percent of the time, most researchers would concludethat Drug X really works (or at least, that there is evidence favoringthe conclusion that it works).
Now suppose Drug Y also outperformed the placebo, but by anamount that would be expected by chance 6 percent of the time. Inthat case, conventional analysis would say that such an effect lackedstatistical significance and that there was insufficient evidence toconclude that Drug Y worked.
If both drugs were tested on the same disease, though, a conundrumarises. For even though Drug X appeared to work at a statisticallysignificant level and Drug Y did not, the difference between theperformance of Drug A and Drug B might very well NOT bestatistically significant. Had they been tested against each other,rather than separately against placebos, there may have been nostatistical evidence to suggest that one was better than the other(even if their cure rates had been precisely the same as in theseparate tests).
"Comparisons of the sort, ‘X is statistically significant but Y is not,'can be misleading," statisticians Andrew Gelman of ColumbiaUniversity and Hal Stern of the University of California, Irvine, notedin an article discussing this issue in 2006 in the AmericanStatistician. "Students and practitioners [should] be made moreaware that the difference between ‘significant' and ‘not significant' isnot itself statistically significant." A similar real-life example arises in studies suggesting that childrenand adolescents taking antidepressants face an increased risk ofsuicidal thoughts or behavior. Most such studies show no statisticallysignificant increase in such risk, but some show a small (possiblydue to chance) excess of suicidal behavior in groups receiving thedrug rather than a placebo. One set of such studies, for instance,found that with the antidepressant Paxil, trials recorded more thantwice the rate of suicidal incidents for participants given the drugcompared with those given the placebo. For another antidepressant,Prozac, trials found fewer suicidal incidents with the drug than withthe placebo. So it appeared that Paxil might be more dangerous thanProzac.
But actually, the rate of suicidal incidents was higher with Prozacthan with Paxil. The apparent safety advantage of Prozac was duenot to the behavior of kids on the drug, but to kids on placebo — inthe Paxil trials, fewer kids on placebo reported incidents than thoseon placebo in the Prozac trials. So the original evidence for showinga possible danger signal from Paxil but not from Prozac was based ondata from people in two placebo groups, none of whom receivedeither drug. Consequently it can be misleading to use statisticalsignificance results alone when comparing the benefits (or dangers)of two drugs.
BOX 2: The Hunger Hypothesis A common misinterpretation of the statistician's P value is that itmeasures how likely it is that a null (or "no effect") hypothesis iscorrect. Actually, the P value gives the probability of observing aresult if the null hypothesis is true, and there is no real effect of atreatment or difference between groups being tested. A P value of.05, for instance, means that there is only a 5 percent chance of getting the observed results if the null hypothesis is correct.
It is incorrect, however, to transpose that finding into a 95 percentprobability that the null hypothesis is false. "The P value iscalculated under the assumption that the null hypothesis is true,"writes biostatistician Steven Goodman. "It therefore cannotsimultaneously be a probability that the null hypothesis is false." Consider this simplified example. Suppose a certain dog is known tobark constantly when hungry. But when well-fed, the dog barks lessthan 5 percent of the time. So if you assume for the null hypothesisthat the dog is not hungry, the probability of observing the dogbarking (given that hypothesis) is less than 5 percent. If you thenactually do observe the dog barking, what is the likelihood that thenull hypothesis is incorrect and the dog is in fact hungry? Answer: That probability cannot be computed with the informationgiven. The dog barks 100 percent of the time when hungry, and lessthan 5 percent of the time when not hungry. To compute thelikelihood of hunger, you need to know how often the dog is fed,information not provided by the mere observation of barking.
BOX 3: Randomness and Clinical Trials Assigning patients at random to treatment and control groups is anessential feature of controlled clinical trials, but statistically thatapproach cannot guarantee that individual differences amongpatients will always be distributed equally. Experts in clinical trialanalyses are aware that such incomplete randomization will leavesome important differences unbalanced between experimentalgroups, at least some of the time.
"This is an important concern," says biostatistician Don Berry of M.D.
Anderson Cancer Center in Houston.
In an e-mail message, Berry points out that two patients who appearto be alike may respond differently to identical treatments. Sostatisticians attempt to incorporate patient variability into theirmathematical models.
"There may be a googol of patient characteristics and it's guaranteedthat not all of them will be balanced by randomization," Berry notes.
"But some characteristics will be biased in favor of treatment A andothers in favor of treatment B. They tend to even out. What is notevened out is regarded by statisticians to be ‘random error,' and thiswe model explicitly." Understanding the individual differences affecting response totreatment is a major goal of scientists pursuing "personalizedmedicine," in which therapies are tailored to each person's particularbiology. But the limits of statistical methods in drawing conclusions about subgroups of patients pose a challenge to achieving that goal.
"False-positive observations abound," Berry acknowledges. "Thereare patients whose tumors melt away when given some of our newertreatments.… But just which one of the googol of characteristics ofthis particular tumor enabled such a thing? It's like looking for aneedle in a haystack . or rather, looking for one special needle in astack of other needles." BOX 4: Bayesian Reasoning Bayesian methods of statistical analysis stem from a paper publishedposthumously in 1763 by the English clergyman Thomas Bayes. In aBayesian analysis, probability calculations require a prior value forthe likelihood of an association, which is then modified after data arecollected. When the prior probability isn't known, it must beestimated, leading to criticisms that subjective guesses must oftenbe incorporated into what ought to be an objective scientific analysis.
But without such an estimate, statistics can produce grosslyinaccurate conclusions.
For a simplified example, consider the use of drug tests to detectcheaters in sports. Suppose the test for steroid use among baseballplayers is 95 percent accurate — that is, it correctly identifies actualsteroid users 95 percent of the time, and misidentifies non-users asusers 5 percent of the time.
Suppose an anonymous player tests positive. What is the probabilitythat he really is using steroids? Since the test really is accurate 95percent of the time, the naïve answer would be that probability ofguilt is 95 percent. But a Bayesian knows that such a conclusioncannot be drawn from the test alone. You would need to know someadditional facts not included in this evidence. In this case, you needto know how many baseball players use steroids to begin with — thatwould be what a Bayesian would call the prior probability.
Now suppose, based on previous testing, that experts haveestablished that about 5 percent of professional baseball players usesteroids. Now suppose you test 400 players. How many would testpositive? • Out of the 400 players, 20 are users (5 percent) and 380 are notusers.
• Of the 20 users, 19 (95 percent) would be identified correctly asusers.
• Of the 380 nonusers, 19 (5 percent) would incorrectly be indicatedas users.
So if you tested 400 players, 38 would test positive. Of those, 19would be guilty users and 19 would be innocent nonusers. So if anysingle player's test is positive, the chances that he really is a user are 50 percent, since an equal number of users and nonusers testpositive.
SUGGESTED READING :
Bower, B. 1997. Null science: Psychology's statistical status quo drawsfire. Science News 151:356-357.
Nuzzo, R. 2008. Nabbing suspicious SNPs. Science News 173(June21):20-24.
CITATIONS & REFERENCES :
Berry, D.A. 2006. Bayesian cinical trials. Nature Reviews DrugDiscovery 5(January:27-36.
Berry, D.A. 2007. The difficult and ubiquitous problems ofmultiplicities. Pharmaceutical Statistics 6:155-160.
Altman, D.G. 1994. The scandal of poor medical research. BritishMedical Journal 308:283-284.
Berger, V.W., and S. Weinstein. 2004. Ensuring the comparability ofcomparison groups: Is randomization enough? Controlled Clinical Trials25.
Diamond, G.A., and S. Kaul. 2004. Prior convictions: Bayesianapproaches to the analysis and interpretation of clinical megatrials.
Journal of the American College of Cardiology 43:1929-1939.
Gelman, A., and D. Weaklie. 2009. Of beauty, sex and power. AmericanScientist 97:310-316.
Gelman, A., and H. Stern. 2006. The difference between ‘significant'and ‘not significant' is not itself statistically significant. AmericanStatistictian 60(November):328-331.
Goodman, S.N. 1999. Toward evidence-based medical statistics. 1:The P Value Fallacy." Annals of Internal Medicine 130(June15):995-1004.
Goodman, S.N. 2008. A dirty dozen: Twelve P-value misconceptions.
Seminars in Hematology 45:135-140.
doi:10.1053/j.seminhematol.2008.04.003.
Hennekens, C.H., and D. DeMets. 2009. The need for large-scalerandomized evidence without undue emphasis on small trials,meta-analyses, or subgroup analyses. Journal of the American MedicalAssociation 302(Dec. 2):2361-2362.
Hubbard, R., and J. Scott Armstrong. 2006. Why we don't really knowwhat ‘statistical significance' means: A major educational failure.
Journal of Marketing Education 28(August):114-120.
Hubbard, R., and R. Murray Lindsey. 2008. Why P values are not auseful measure of evidence in statistical significance testing. Theory &Psychology 18:69-88.
Ioannidis, J.P.A. 2005. Why most published research findings are false.
PLoS Medicine 2(August):0101-0106.
Kent, D., and R. Hayward. 2007. When averages hide individualdifferences in clinical trials. American Scientist 95(January- February):60. DOI: 10.1511/2007.63.1016 Morgan, T.H., et al. 2007. Nonvalidation of reported genetic risk factorsfor acute coronary syndrome in a large-scale replication study. Journalof the American Medical Association 297(April 11):1551-1561.
Nuzzo, R. 2008. Nabbing suspicious SNPs. Science News 173(June21):20-24.
Psaty, B.M., and C.D. Furberg. 2007. Rosiglitazone and cardiovascularrisk. New England Journal of Medicine 356:2522-2524.
Stephens, P.A., S.W. Buskirk, and C. Martínez del Rio. 2007. Inferencein ecology and evolution. Trends in Ecology and Evolution 22(April1):192-197.
Stroup, T.S., et al. 2006. Clinical trials for antipsychotic drugs: Designconventions, dilemmas and innovations. Nature Reviews DrugDiscovery 5(February):133-146.
Sullivan, P.F. 2006. Spurious genetic associations. BiologicalPsychiatry 61:1121-1126. doi:10.1016/j.biopsych.2006.11.010 Wacholder, S., et al. 2004. Assessing the probability that a positivereport is false: An approach for molecular epidemiology studies.
Journal of the National Cancer Institute 96(March 17):434-442.
Howson, C., and P. Urbach. 2006. Scientific Reasoning: The BayesianApproach. Third Edition. Chicago: Open Court.
Salsburg, D. 2001. The Lady Tasting Tea. New York: W.H. Freeman.
Ziliak, S.T., and D. McCloskey. 2008. The Cult of StatisticalSignificance. University of Michigan Press.

Source: http://www2.iona.edu/faculty/rlavelle/math270/Odds%20Are,%20It's%20Wrong%20-%20Science%20News.pdf